機器人也需要碰撞標準?
當我們評價一款車的安全性時,經常會以碰撞測試成績作為一個主要的參考項。始于1997年的NCAP為提升汽車的被動安全性做出了巨大貢獻,在此之前,由于沒有明確的汽車安全設計和測試標準,導致各大廠商要不對安全指標不關心,要不就按照自己的理解來做,因此在九十年代末期進行的NCAP測試中,幾乎所有車型的成績都在3星以下,按照今天的平均水平來看的話是非常差的。
設計指導思想的差異,導致1998年款奧迪A6的碰撞成績還不如2006年款標致207:

▲1998年款A6(C5),碰撞三星,中國市場上第一批圓頭圓腦的A6L即源自這一代,至今還能在街上看到。
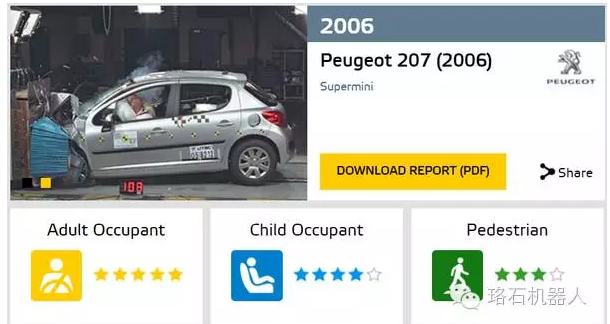
▲小巧的標致207。大約從2006年開始,市面上銷售的大部分合資微型車成績已經到5星了。
標準的進步促使廠商修改了產品需求和設計目標,從而為我們提供更為安全的汽車,讓人們更安全的享受汽車帶來的便利。
長期以來,機器人行業標準里有關機器與人之間如何安全交互的內容一直缺失,大部分都是“在使用機器人之前,應進行安全評估以保證人員安全”之類的模糊描述。
隨著ISO 15066的出現,機器人行業第一次有了自己的“碰撞標準”。
在讓機器人更安全(三)中,我們講到協作機器人最重要的一種協作方式是Power and force limiting (功率和力限制),那么對于具備這一特性的機器人來講,究竟把功率和力的大小限制到何等程度才算是安全呢?
既然協作機器人強調的是“人機”協作,那么很自然我們可以想到: 機器與人發生碰撞時,能夠保證人體不受疼痛/傷害影響的值是才是安全的。看上去像是一句廢話,但其實它傳達了ISO15066的一個核心的理念:
if contact between robots and humans is allowed,and incidental contact does occur,then that contact shall not result in pain or injury.要想獲得這個安全的值,我們需要一個前提假設:符合碰撞標準的機器人能量最大值可以根據人類的疼痛閾值(pain sensitivity thresholds)計算出來。
要實現這個前提,我們需要:
人體模型(human body model)
人體各部位對安全的要求是不同的,需要分區域對待;
疼痛閾值(pain sensitivity thresholds)
以力(N)/壓強(N/cm^2)/能量(J)的方式來定義或反映該閾值;
碰撞模型及計算方法
提供一個可用度和復雜度相對平衡的換算機制,這個機制結合上面的數據,就可以反求出機器人的運動限制;
根據以上信息,我們就可以得到一系列在設計、部署機器人時的限制數據,用于指導機器人的開發和使用。
人體模型與疼痛閾值
上圖是亂入的,這里我們只要用到生物力學(biomechanical)的一些簡單知識(生物學的不好,不知道是不是這么翻譯。。。)。
ISO15066里用到的人體模型比較簡單,只把人體劃分為26個區域,有的區域會區分一下身體的前后,見下圖中紅點標識的地方,原圖的清晰度不高,見諒。
▼▼ 看圖說話,比比誰認識的醫學名詞多~
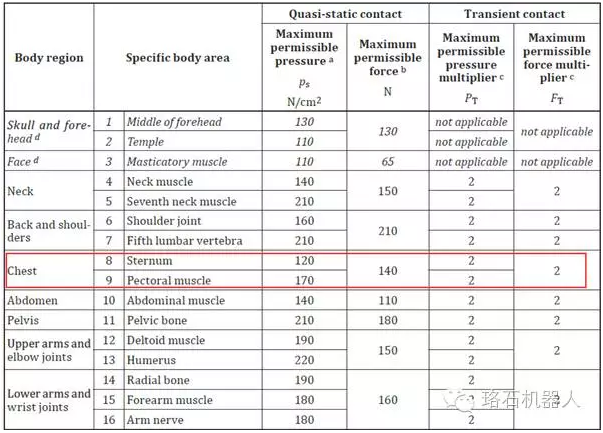
以上引用的Biomechanical數據來源于University of Mainz的一項關于協作機器人與人員碰撞數據的專項研究,這項研究中使用了100名身體健康的成年實驗對象,分別對上述26個區域進行單獨的疼痛測試,下面表格中的最大值是使75%測試人員開始感覺疼痛的值(節選):
▲在準靜態和瞬態接觸兩種情況下,人體不同區域對于產生疼痛感時的壓強和力的閾值。
這么多數據看起來有沒有一種很頭疼的感覺。
其實表格的內容很簡單,就是整個實驗過程的一個數據統計,把人體各部位在準靜態接觸和瞬態接觸兩種情況下所能允許的壓強和壓力分別列出來而已。這個數值,是人體開始感覺到疼痛的閾值(Pain Onset Level)。
例如,以胸部區域(Chest)為例,在準靜態接觸時,胸骨和胸肌所能允許的最大壓強分別為120N/cm^2和170N/cm^2,最大壓力為140N;而在瞬態接觸時,以上數值最多可以乘以2倍(Multiplier,乘子)。
胸骨比胸肌所能承受的壓強小,很容易理解,回想一下小腿骨前部磕到桌子時的感受。
沒磕過的歡迎去嘗試一下,其實也沒啥,可以增添一些美好回憶。
上表中給出壓強和力兩個數值,是因為有些時候力不大,但是壓強很大,反之亦然。
在UR機器人的宣傳資料中,有這么一句話:
in a collision, the robot delivers less force than the 150 Newton.
50N的數值,基本上可以滿足上面表格中絕大部分的情況,是一個相對安全的數值。
ok,數值有了,那么在部署機器人系統時,怎么換算成機器人的運動限制呢(速度/功率)?
計算運動限制
首先,對于準靜態接觸來說,可以直接通過機器人內置的測量機制(力/力矩傳感器,末端力估計等)來判斷機器人對外輸出的靜力是否超過限制。
對于瞬態接觸,情況要稍微復雜一些。
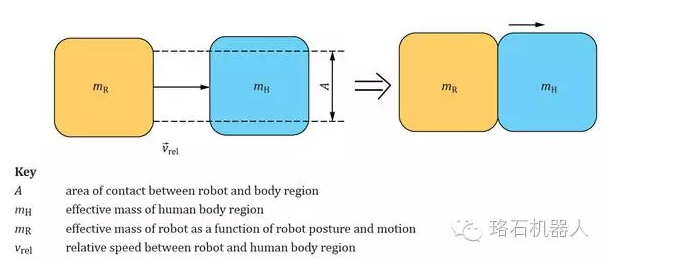
由于涉及到碰撞,因此我們需要一個碰撞模型。在ISO 15066中把機器人和人員之間的碰撞用一個簡化的非彈性碰撞模型來描述:
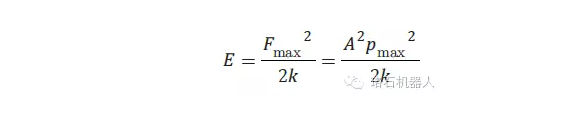
▲ 等效碰撞模型,A是碰撞面積;mH是碰撞區域中的人體有效質量;mR是機器人的有效質量,是機器人姿態和運動的函數;Vrel是二者的相對速度。
出于計算需要,我們還需要得到人體各部位的有效質量和有效彈性常數: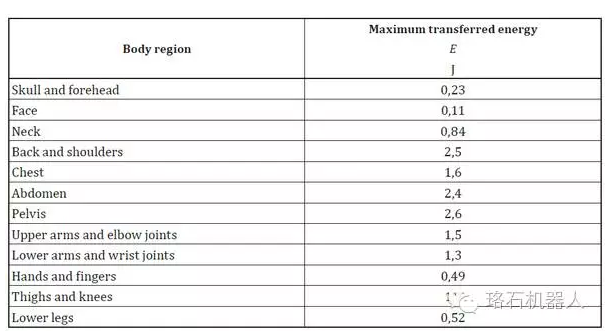
▲ 人體不同區域有效彈性系數與有效質量,用于計算各區域所能承受的最大能量值。
(之后使用的數據和計算中,碰撞面積A為1cm^2)
對于每一個區域而言,碰撞時允許傳遞的最大能量可以用下式來計算:
其中,E是所允許傳遞的最大能力,Fmax和Pmax是上面提到的最大允許壓力和壓強,A是接觸面積,k是彈性常數,將該式應用于上表,可以獲得人體不同區域,引起疼痛時的能量閾值:
▲ 在人體各主要部位上引起疼痛的能量閾值。
但是能量這個東西不好理解,在機器人上也不好進行限制,因此我們需要把它進行一下處理,轉換成機器人經常使用的參數:速度。
基于完全非彈性碰撞的假設,我們可以得到下列式子(對數學不感興趣的同學可以直接跳過到后面 展望 的章節):
▲ 上述三個式子中,μ是two-body系統的折算質量,mH是人體的有效質量,mR是機器人的有效質量。
對于機器人的簡化模型,可以使用下圖來表示
▲ 上圖中,mL是機器人的有效負載,包括工具和工件,M是機器人所有運動部件的總質量,ω是旋轉角速度。
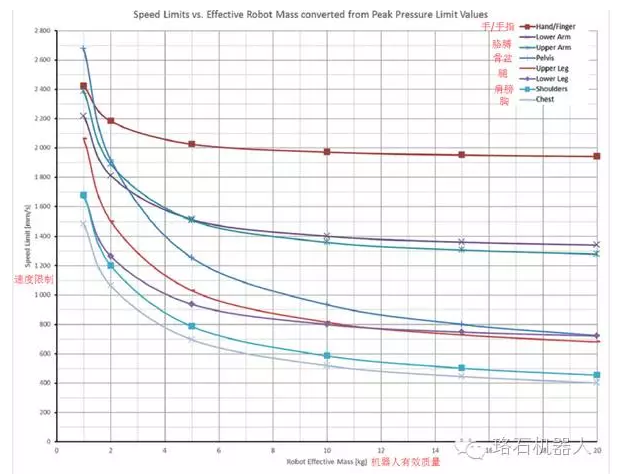
聯立A.2~A.5,我們終于可以得到機器人的最大允許速度:應用式子A.6,我們可以計算出一個示例,來表示在接觸面積為1cm^2時,機器人質量和最大允許速度之間的關系:
▲ 可以看到,如果機器人的運動有效質量為20kg(目前絕大多數小型機器人的質量都在20kg附近),接觸面積為1cm^2,主要碰撞區域為手臂時,最大速度應不超過1.4m/s。
這個例子中,接觸面積為1cm^2,而在實際使用中,接觸面積應取機器人和人員面積較小的一個,面積越小,壓強越大,這也是為什么協作機器人的表面都很圓滑,不會出現尖銳邊緣的原因。
展望
ISO 15066目前只是一個TS(Technical Specification),還不是一個正式的標準(Standard),里面提供了目前所知最新的關于協作機器人的設計準則和安全標準,但是技術進步如此迅速,在以后的時間里根據最新的科研/產業成果更新內容的可能性很大。
完整讀完上述內容的讀者應該發現,ISO 15066提供的碰撞標準相對來講是比較簡陋的,對實際情況做了很多理想的假設和簡化,這也是未來新的標準需要細化完善的地方。
除此之外,相對于機器人這樣一個比較確定的系統,“人”的因素就顯得非常多變。在人體模型和疼痛閾值研究中就發現,不同的人每個區域采集到的數據上下限差距很大,例如對于食指來講,100個人平均閾值為58N,最低為35N,最高為102N。
而且該項研究僅適用于健康的成年人,不適用于體弱多病的人(sick people),不適用于兒童。因此,整個機器人的安全工作任重而道遠。